虽然计算机能极快地进行运算，但其内部并不像人类在实际生活中使用各种不同的数据类型—文字、数字、声音，图像等，而是使用只包含0和1两个数值的二进制。

当然，人们输入计算机的数据被转换成二进制进行计算，计算后的结果又由二进制转换成文字、整数、小数等，这都由操作系统自动完成，并不需要人们手工去做，想要了解数据在计算机内的存储方式，就必须了解二进制（还有八进制/十六进制）。

人们通常采用的数制有十进制、二进制、八进制和十六进制。

我们最常用的数制是十进制，我们熟悉的十进制是由0，1，2，3，4，5，6，7，8，9这十个符号来描述，计数规则是逢十进一，比如：10（请读作一零）表示的是十。

与此类似，二进制由1、0两个符号来表示，计数规则是逢二进一，比如：10表示的是二，11表示的是三，100表示的是四。

十六进制是由0，1，2，3，4，5，6，7，8，9，A，B，C，D，E，F表示，计数规则是逢十六进一，比如：A表示的是十，F表示的是十五，3F表示的是六十三。

1.掌握二进制、十进制、十六进制的之间的相互转换。

2.掌握二进制的具体应用，并能解释诸多IT领域常见限制。

3.掌握“模”的概念及原码，反码与补码的基本概念。

1.十进制表示法

对于十进制整数32785来说，可以通过加法，乘法与次方运算表示为：

32785 = 3*10^4 + 2*10^3 + 7*10^2 + 8*10^1 + 5*10^0

对于十进制小数8693.357来说，则可以表示为：

8693.457 = 8*10^3 + 6*10^2 + 9*10^1 + 3*10^0 + 4*10^-1 + 5*10^-2 + 7*10^-3

2.二进制表示法

对于二进制整数10101011来说，参考十进制表示法，可表示为：

10101011 = 1*2^7 + 0*2^6 + 1*2^5 + 0*2^4 + 1*2^3 + 0*2^2 + 1*2^1 + 1*2^0

        = 128 + 0 + 32 + 0 + 8 + 0 + 2 + 1 = 171

这也是二进制转十进制的基本方法。

那么对于二进制小数来说，我们也同样参考上述表示方法，比如：

1101.101 = 1*2^3 + 1*2^2 + 0*2^1 + 1*2^0 + 1*2^-1 + 0*2^-2 + 1*2^-3

        = 8 + 4 + 0 + 1 + 0.5 + 0 + 0.125 = 13.625

3.十六进制表示法

D3A8 = D*16^3 + 3*16^2 + A*16^1 + 8*16^0

= 13*4096 + 3*256 + 10*16 + 8 = 54184

4.十进制转二进制

十进制整数转二进制整数，其关键点在于：“逢二进一，倒过来”，即：将一个十进制数除以二，得到的商再除以二，依此类推直到商等于一或零时为止，倒序取除得的余数，即换算为二进制数的结果

例如把52换算成二进制数，计算结果如图：如下：

52除以2得到的余数依次为：0、0、1、0、1、1，倒序排列，所以52对应的二进制数就是110100。

那么对于十进制小数转换为二进制是，则实行“乘二取整，顺着来”，即将该十进制的小数部分乘以2，取得整数部分（为0或为1），再将其小数部分继续乘以2，直到最后整数部分和小数部分均为0为止。（当然，也有可能一直无法取得0，要么无限循环，要么无限不循环，那么此时，该小数在计算机当中的运算可能出现精度丢失的问题）。

比如十进制小数0.3125，对应的二进制表达式为：

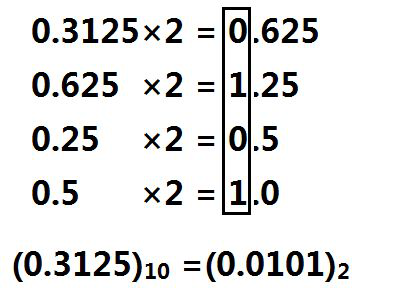
我们不妨再来看看，对于小数0.4来说，其对应的十进制表达式为：

我们可以看到，乘到最后，又回到了0.4，所以这是一个无限循环的二进制。其二进制可表示为：

0.01100110……（循环0110），那么，此时，计算机会怎么处理这种无限的小数呢？后续实验我们来为大家揭晓答案。

5.十进制转十六进制

与二进制一样，对于整数和小数的运算方法完全一致。

6.二进制与十六进制互转

事实上，在计算机中，二进制与十六进制是完全等价的，两者本质上没有任何区别。

通常为了保持一定的可读性，我们更习惯用十六进制来表示计算机机器码，而并非二进制。

当然，由于两者没有任何区别，所以我们不用特别在意。由于16正好是2的4次方，所以我们只需要简单地将4位二进制放在一起，就转换成了一位十六进制。转换过程一一对应即可：

0000（0） 0001 （1） 0010 （2） 0011 （3） 0100 （4） 0101 （5）

0110 （6） 0111 （7） 1000 （8） 1001 （9） 1010（A） 1011 （B）

1100 （C） 1101 （D） 1110 （E） 1111 （F）

那么，如果只有6位二进制应该怎么处理呢？

很简单，在这6位十进制的前面加两个0，变成8位，再进行等价转换即可。

7.原码，反码与补码

(1).机器数：

一个数在计算机中的二进制表示形式, ，叫做这个数的机器数。机器数是带符号的，在计算机用一个数的最高位存放符号,，正数为0， 负数为1。

比如，十进制中的数 +3 ，计算机字长为8位，转换成二进制就是00000011。如果是 -3 ，就是 10000011 。那么，这里的 00000011 和 10000011 就是机器数。

(2).真值：

因为第一位是符号位，所以机器数的形式值就不等于真正的数值。例如上面的有符号数 10000011，其最高位1代表负，其真正数值是 -3 而不是形式值131（10000011转换成十进制等于131）。所以，为区别起见，将带符号位的机器数对应的真正数值称为机器数的真值。

例：0000 0001的真值 = +000 0001 = +1，1000 0001的真值 = –000 0001 = –1

(3).原码：

原码就是符号位加上真值的绝对值, 即用第一位表示符号, 其余位表示值. 比如如果是8位二进制：

    [+1]原 = 0000 0001

    [-1]原 = 1000 0001

第一位是符号位. 因为第一位是符号位, 所以8位二进制数的取值范围就是：

    [1111 1111，0111 1111]

即  [-127 , 127]

原码是人脑最容易理解和计算的表示方式。

(4).反码：

反码的表示方法是：正数的反码是其本身，负数的反码是在其原码的基础上, 符号位不变，其余各个位取反。如：

    [+1] = [00000001]原 = [00000001]反

    [-1] = [10000001]原 = [11111110]反

可见如果一个反码表示的是负数, 人脑无法直观的看出来它的数值. 通常要将其转换成原码再计算。

(5).补码：

补码的表示方法是：正数的补码就是其本身，负数的补码是在其原码的基础上, 符号位不变, 其余各位取反, 最后+1。(即在反码的基础上+1)，如：

    [+1] = [00000001]原 = [00000001]反 = [00000001]补

    [-1] = [10000001]原 = [11111110]反 = [11111111]补

对于负数, 补码表示方式也是人脑无法直观看出其数值的，通常也需要转换成原码在计算其数值。

(6).计算机的减法计算：

现在我们知道了计算机可以有三种编码方式表示一个数。 对于正数因为三种编码方式的结果都相同:

    [+1] = [00000001]原 = [00000001]反 = [00000001]补

所以不需要过多解释。 但是对于负数:

    [-1] = [10000001]原 = [11111110]反 = [11111111]补

可见原码， 反码和补码是完全不同的。 既然原码才是被人脑直接识别并用于计算表示方式， 为何还会有反码和补码呢?

首先， 因为人脑可以知道第一位是符号位， 在计算的时候我们会根据符号位， 选择对真值区域的加减。 (真值的概念在本文最开头)。 但是对于计算机， 加减乘数已经是最基础的运算， 要设计的尽量简单。 计算机辨别"符号位"显然会让计算机的基础电路设计变得十分复杂! 于是人们想出了将符号位也参与运算的方法。 我们知道， 根据运算法则减去一个正数等于加上一个负数， 即: 1-1 = 1 + (-1) = 0 ， 所以机器可以只有加法而没有减法， 这样计算机运算的设计就更简单了。

于是人们开始探索 将符号位参与运算， 并且只保留加法的方法。 首先来看原码:

计算十进制的表达式: 1-1=0

    1 - 1 = 1 + (-1) = [00000001]原 + [10000001]原 = [10000010]原 = -2

如果用原码表示， 让符号位也参与计算， 显然对于减法来说， 结果是不正确的。这也就是为何计算机内部不使用原码表示一个数。

为了解决原码做减法的问题， 出现了反码:

计算十进制的表达式: 1-1=0

    1 - 1 = 1 + (-1) = [0000 0001]原 + [1000 0001]原= [0000 0001]反 + [1111 1110]反 = [1111 1111]反 = [1000 0000]原 = -0

发现用反码计算减法， 结果的真值部分是正确的。 而唯一的问题其实就出现在"0"这个特殊的数值上。 虽然人们理解上+0和-0是一样的， 但是0带符号是没有任何意义的。 而且会有[0000 0000]原和[1000 0000]原两个编码表示0。

于是补码的出现， 解决了0的符号以及两个编码的问题:

    1-1 = 1 + (-1) = [0000 0001]原 + [1000 0001]原 = [0000 0001]补 + [1111 1111]补 = [0000 0000]补=[0000 0000]原

这样0用[0000 0000]表示， 而以前出现问题的-0则不存在了。而且可以用[1000 0000]表示-128:

    (-1) + (-127) = [1000 0001]原 + [1111 1111]原 = [1111 1111]补 + [1000 0001]补 = [1000 0000]补

-1-127的结果应该是-128， 在用补码运算的结果中， [1000 0000]补 就是-128。 但是注意因为实际上是使用以前的-0的补码来表示-128， 所以-128并没有原码和反码表示。(对-128的补码表示[1000 0000]补算出来的原码是[0000 0000]原， 这是不正确的)

使用补码， 不仅仅修复了0的符号以及存在两个编码的问题， 而且还能够多表示一个最低数。 这就是为什么8位二进制， 使用原码或反码表示的范围为[-127， +127]， 而使用补码表示的范围为[-128， 127]。

8.模

将钟表想象成是一个1位的12进制数，如果当前时间是10点，我希望将时间设置成6点，需要怎么做呢？

我们可以：

(1) 往回拨4个小时：10 - 4 = 6

(2) 往前拨8个小时：(10 + 8) mod 12 = 6

(3) 往前拨8+12=20个小时: (10+20) mod 12 = 6

在第二，第三种方法中的mod是指取模操作, 18 mod 12 = 6 即用18除以12后的余数是6。

所以钟表往回拨(减法)的结果可以用往前拨(加法)替代。

而计算机就是通过类似的原理将减法替换成加法作计算。

9.位移：

1000 左移2位 -> 100000，即8 << 2 = 32，所以可知，在范围允许的情况下，左移1位即乘以2。

1000 右称2位 -> 10，即8 >> 2 = 2，即右移1位即除以2。

所以在计算机中，乘法和除法通过位移进行运算，快速方便。

1.为什么32位的操作系统最大只能支持4G的内存？

2.为什么经常听说现在的IP地址快不够用了？

3.为什么中文在操作系统当中要占用2个字节？

4.25 * 10，如何通过位移运算或加法运算来获得结果？

5.自行查阅相关资料了解八进制及其转换。

下周推送：预备知识：Java程序设计基础->数组

为了答谢大家对蜗牛学院的支持，蜗牛学院将会定期对大家免费发放干货，敬请关注蜗牛学院的官方微信。